4.2. Algorithm Syntax

An algorithm is dedicated to be run by an abstract machine similar to a computer but without its physical limits. This abstract machine is composed by:

  • A processor: this is the executing unit (can be the analyst)

  • A memory: to store data and instructions (can be a simple sheet)

  • Input and Output devices: to permits communication (can be reading or printing a variable)

The processor execute the instructions as specified in the algorithm and data and instructions are stored in the infinite memory (we don’t care about their physical representations).

This section gives writting conventions that should be seen as an “algorithm vocabulary”. An algorithm should be structured as:

Algorithm <id_algorithm>
------------------------
Description
  <Comments to explain goals, and conditions to run the algorithm correctly>
------------------------
Constants
  <id_constant> = <expression>
  ...
Functions
  <id_function> (<id_param> : <id_type>, ...)
  ...
Variables
  <id_variable> : <id_type>
  ...
Start
  <instructions>
  ...
End

We will consider as mandatory:

  • The name of algorithm

  • the Description block that is a comment to help the user to understand the algorithm and how to use it. It includes desription for inputs/outputs.

  • the Start/End block contains instructions (that can be structured in different instructions blocks)

Others part of the algorithm are facultative and depends on its complexity and on the solved problem.

4.2.1. A first example

Consider the following algorithm as a basic example:

Listing 4.1: conversion algorithm
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
Algorithm convertTemperatureCtoK
--------------------------------
Description
  Print temperature in Kelvin from input read temperature in Celcius
--------------------------------
Constants
  zeroC = 273.15
Variables
  tempC : real
  tempK : real
Start
  Print("Enter temperature in Celcius :")
  Read(tempC)
  tempK <- tempC + zeroC
  Print(tempC, "°C is ", tempK, "K")
End

Some programming languages will be study in details in following lessons, but it is already interesting to look for this algorithm transcription in different programming languages:

Listing 4.2: convertTemperatureCtoK.c
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
//convertTemperatureCtoK
//----------------------
//Print temperature in Kelvin from input read temperature in Celcius
#include <stdio.h>
main()
{
  const float zeroC(273.15);
  float tempC,tempK;
  printf("Enter temperature in Celcius :\n");
  scanf(&tempC);
  tempK = tempC + zeroC;
  printf("%f °C is %f K\n", tempC, tempK);
}
Listing 4.3: convertTemperatureCtoK.cpp
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
//convertTemperatureCtoK
//----------------------
//Print temperature in Kelvin from input read temperature in Celcius
#include <iostream>
main()
{
  const float zeroC(273.15);
  float tempC,tempK;
  std::cout << "Enter temperature in Celcius :" << std::endl;
  std::cin >> tempC;
  tempK = tempC + zeroC;
  std::cout << tempC << " °C is " << tempK << " K" << std::endl;
}
Listing 4.4: convertTemperatureCtoK.py
1
2
3
4
5
6
7
8
9
#convertTemperatureCtoK
#----------------------
#Print temperature in Kelvin from input read temperature in Celcius
# -*-coding:utf8 -*
zeroC = 273.15
tempC = input("Enter temperature in Celcius :")
tempC = float(tempC)
tempK = tempC + zeroC
print(tempC, " °C is ", tempK, " K")
Listing 4.5: convertTemperatureCtoK.f90
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
!convertTemperatureCtoK
!----------------------
!Print temperature in Kelvin from input read temperature in Celcius
PROGRAM convertTemperatureCtoK
  IMPLICIT NONE
  REAL, PARAMETER :: zeroC = 273.15d0
  REAL :: tempC, tempK
  PRINT*, "Enter temperature in Celcius :"
  READ*, tempC
  tempK = tempC + zeroC
  PRINT*, tempC, " °C is ", tempK, " K"
END PROGRAM convertTemperatureCtoK

4.2.2. Data types

In algorithms, data types (integer, real, etc.) are important since they determine the possible operations that can be perfomed on data (i.e. euclidian division or real division produce different results). Variables definitions should include data type.

4.2.2.1. Primitive types

These primitive types of data are generally available whatever the programming language is. For algorithmic purpose, we will retain: boolean, integer, float and character.

Listing 4.6: four variables with different identifier and different types
Variables
  testVar : boolean
  n : integer
  f : float
  c : character

4.2.2.2. Composite types

When a lot of data of the same type are required, they are grouped in composite types as arrays. A string is a specific array of character.

Listing 4.7: defining different arrays in algorithms and operations
Variables
  myArray : array[50] of integer
  myString : string[3]
  sentence : "algorithm is not so difficult"    / A string with 29 characters (+ 0 for ending)
Start
  myArray[0] <- 42
  myString[0] <- 'O'
  myString[1] <- 'K'
  myString[2] <- 0     /Code for end of the string
End

Other composite types exist and may be used depending on the programming language used: list, tuple, dictionary, stack, tree, graph, objects, etc.

Caution

Arrays are accessed using the formalisme arrayName[indice]. We use the convention that a n size array always begin by indice 0 and finishes by indice n-1.

4.2.3. Predefined operators and mathematical functions

Algorithm operations are done thanks to predefined operators and functions that can be used directly in algorithms: -, +, *, /, \%, abs, sqrt, cos, sin, etc.

Listing 4.8: some basic operations and printing
Variables
  n, i : integer
Start
  Print("Euclidian division of n by i. Quotient: ", n/i, " remainder: ", n%i)
  Print(" pi: ", 4*atan(-1.))
End

4.2.4. Instructions

Instructions are generally executed sequentially, that is to say step-by-step from top to bottom in the algorithm sequence. But some structured instructions as conditional and repetitive instructions will modify this sequence. Here are described the basic instructions that are used in algorithm.

4.2.4.1. Affectation

The affectation consists in attributing a value to a given variable. This is done thanks to the arrow symbol \leftarrow (<-).

Listing 4.9: some affectations
Variables
  i : integer
  f : float
  c : character
  b : boolean
Start
  i <- 42
  f <- 3.14
  c <- 'h'
  b <- true (or 0)
End

4.2.4.2. Input/Output

The algorithm is communicating with the rest of the world thanks to input and outputs. We will use mainly Read and Print instructions:

  • the Read instruction allows to get a value from an input (from the keyboard for example) during execution of the algorithm.

  • the Print instruction allows to present the result of the algorithm to an output (can be the screen).

Listing 4.10: Read and Print instructions
Variables
  f : float
Start
  Read(f)
  Print("the value is:", f)
End

4.2.4.3. Conditional instructions

When elementary instructions are used in an algorithm (ie. affectations, inputs/outputs), the execution of the algorithm is sequential. Using conditional instructions permits to modify the execution sequence.

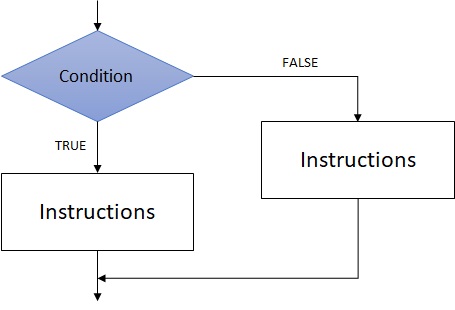
The if conditional instruction allows to switch between two branches in an algorithm. It requires a boolean expression.

if flow chart

_images/if.jpg 
if <boolean expression> then
  <instructions>
else
  <instructions>
endif

Executed instructions depends on the evaluation of the expression: if true, instructions present in the if structure are executed, elsewhere this is the instructions in the else structure that are executed. The else structure is facultative: in that case, if the boolean expression is evaluated as false, nothing appends.

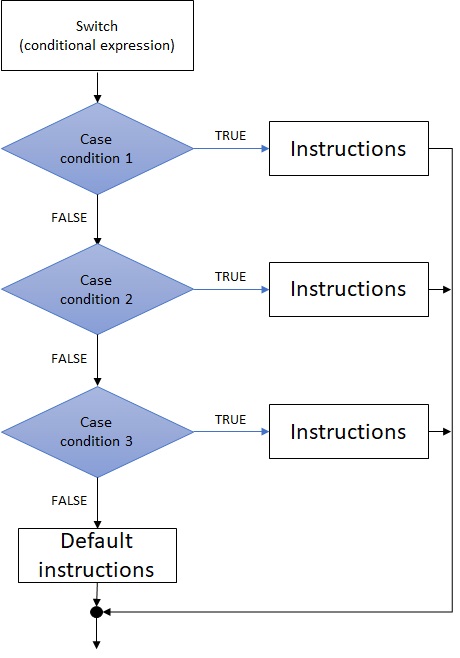
The switch conditional instruction allows to switch between N branches in an algorithm.

switch flow chart

_images/switch.jpg 
switch <expression>
  <case 1> : <instructions>
  <case 2> : <instructions>
  <case 3> : <instructions>
  default : <instructions>
endswitch

Such conditional instruction is usefull to avoid successive if and improve algorithm lisibility. Treating keybord inputs in an application/game is a good example of such conditional instruction utility: the results of the application will depend on the hit key: the left, up, bottom and right key will have different effects on the application.

4.2.4.4. Repetitive instructions

They represent engine of algorithm since if algorithm exists, this is mainly to automatize repetitive human tasks. Two kinds of repetitive instructions (loops) exists.

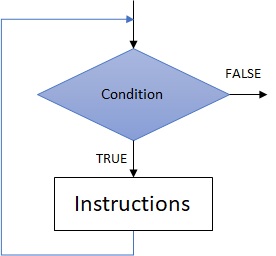
The while loop will execute instructions while an expression is evaluated as true.

while loop flow chart

_images/while.jpg 
while <boolean expression>
  <instructions>
endwhile

This loop is preferabily used when the number of repetitive instructions to do is unknown. One have to take care that the evaluation of the boolean expression can become false, otherwise it will generate an infinite loop.

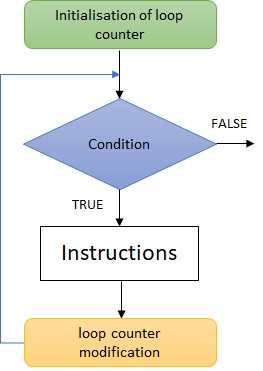
When the number of repetitive instruction to do is known, it is more appropriate to use a for loop.

for loop flow chart

_images/for.jpg 
for <id_variable> from <init_expression> to <final_expression>
  <instructions>
endfor

This loop uses a counter:

  • It is initialised to <init_expression> before the loop.

  • It is automatically increment at each pass trhough the loop (default increment is 1).

  • After counter modification, a condition verifies if the counter reach the <final_expression>. In that case, it exits the loop.

4.2.5. Functions

Functions are used to structure algorithms when they become more complex. They are similar to mathematical functions as they may return an output value from inputs data. A function will have the following structure:

Function <id_function> (<id_param> : <id_type>, ...) : <id_type>
------------------------
Description
  <Comments to explain goals, and conditions to use the function correctly, including input and output descriptions>
------------------------
Constants
  <id_constant> = <expression>
  ...
Functions
  <id_function> (<id_param> : <id_type>, ...)
  ...
Variables
  <id_variable> : <id_type>
  ...
Start
  <instructions>
  ...
  return <expression>
End

An interesting feature of function is that they acts like black boxes for the developer as he only needs to know what are the inputs and output.

_images/function.jpg

Figure 4.3: Schematic representation of a function

Some programming languages make differences between functions and procedures as procedures are not returning any value. This is the case in FORTRAN, but not in C or Python.

4.2.6. Example

To illustrate this section, the following algorithm permits to calcul some statitics on the notes obtained by a group of student to an exam.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Algorithm notesStats
------------------------
Description
  Read notes obtained to an exam by a group of students and calcul some statistics: average, min, max
------------------------
Constants
  NUMBERSTUDENT = 42
Functions
  getNote() : float
  calculAverage (myArray : array of float, size : integer) : float
  calculMax (myArray : array of float, size : integer) : float
  calculMin (myArray : array of float, size : integer) : float
Variables
  etudiants : array[NUMBERSTUDENT] of float
  i : integer
  average, max, min : float

Start
  Print("Exam stats: enter notes for the ", NUMBERSTUDENT, " students.")

  for i from 0 to NUMBERSTUDENT-1
    etudiants[i] <- getNote()
  endfor

  average <- calculAverage(etudiants, NUMBERSTUDENT)
  max <- calculMax(etudiants, NUMBERSTUDENT)
  min <- calculMax(etudiants, NUMBERSTUDENT)

  Print("The average is: ", average)
  Print("The maximum note is: ", max)
  Print("The minimum note is: ", min)
  Print("*****")
End

For example, the function to enter a note can be defined as:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
Function getNote() : float
------------------------
Description
  Return a note entered by user and verifies if in the interval [0;20]
------------------------
Variables
  float note

Start
  do
    Print("Enter note ", i, ":")
    Read(note)
  while(note<0 ou note>20)
  return note
End

It is interesting to note here another use of the while loop. In this last example the loop begins by the do instruction and finishes with the test. This is easy to understand that, in that case, the test is done at the end of the loop. As a consequence, we are sure that the algorithm will execute the instructions in the loop one time before testing the condition. Implementation of this variant of while loop is generally found in the different programming languages.