2.1. Propositional Logic¶

Propositional logic is a branch of logic. It helps to formalize logical problems and to solve it. It also provides the prerequisites to understand the basics of how the integrated circuits used in our computers work. This lesson presents the logical approach and introduces the Boolean algebra.

2.1.1. Intuitive approach¶

A proposition (also named statement) can be true or false. Here are presented some examples of propositions:

1 + 1 = 2
1 + 1 = 3
the weather is sunny today
42 is the answer
Marseille is the capital of France

Caution

Following statements are not propositions:

1 + x = 2 (x being a variable, it is a predicate).

this sentence is false (this can not be true or false).

Propositions can be assembled to form new propositions thanks to “connections”.

It is cloudy AND it is cold
The cat is sleeping OR the mouse is happy

Question

Precise if the following sentences are propositions:

Monkey walk on the moon
A square has 5 sides

2.1.2. Propositional syntax¶

The syntax gives the rules on how to form new propositions using simple statements. This can be seen as the “grammar” of propositional logic.

2.1.2.1. Proposition constant¶

We call proposition constant (or logical constant) a variable belonging to the Boolean domain that contains exactly two values:

$\mathbf{B} = \{true, false\} = \{0, 1\}$

2.1.2.2. Compounds propositions¶

If a proposition constant can be either true (1) or false (0), they can be combined to form new propositions. These new propositions are obtained thanks to different operators: $\lnot$ , $\land$ , $\lor$ , $\Rightarrow$ , $\Leftrightarrow$ and $\oplus$ .

As example, if $p$ , $q$ and $r$ are three proposition constants, we can build thanks to preceeding operators a new compound proposition F also named propositional formula:

(2.1)¶ $F = ((p\land q) \lor (\lnot r)) \Rightarrow p$

2.1.2.3. Vocabulary and language¶

A propositional vocabulary is a set of proposition constants. The set of all compound propositions that can be formed using a vocabulary is named propositional language.

The propositional formula of Eq.2.1: is a compound propositions belonging to the language formed by the vocabulary $\{p,q,r\}$ .

Question

Do the following propositional formulas belong to the propositional language using the vocabulary $\{p,q,r\}$ ?

$F_1 = p \Leftrightarrow r$
$F_2 = r \Rightarrow q \land \lnot s$

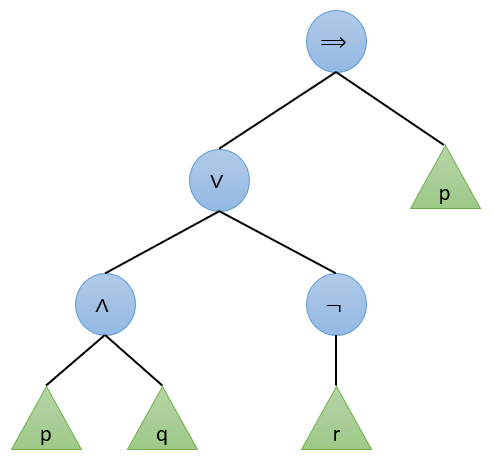
2.1.2.4. Tree representation¶

A propositional formula can also be represented by a tree structure. Here is presented the tree representation of Eq.2.1:

Figure 2.1: Tree representation for example of Eq.2.1.¶

2.1.2.5. Operator precedence¶

To simplify writting of propositional formulae and limit usage of parenthesis, an operator precedence is defined:

operator	precedence
$\lnot$	5
$\land$	4
$\lor$	3
$\oplus$	2
$\Rightarrow$ , $\Leftrightarrow$	1

2.1.3. Propositional semantics¶

Once the syntax being define (rules of grammar), the “meanings” of the symbol used is then defined. This is named semantics.

2.1.3.1. Truth assignment¶

If we consider a propositional vocabulary $\mathcal{V}=\{ p_1, p_2, ..., p_n \}$ of $n$ propositional constants, we call a truth assignment an application such that:

$\begin{array}{cccc} \sigma: & \mathcal{V} & \to & \mathbf{B} \\ & p_1 & \mapsto & ... \\ & p_1 & \mapsto & ... \\ & ... \\ & p_n & \mapsto & ... \end{array}$

For example, we will write that $(p = 1, q=0, r=1)$ is a possible truth assignment of vocabulary $\mathcal{V}=\{ p,q,r \}$ .

For $n=1$ , there are 2 possible truth assignments,
For $n=2$ , there are 4 possible truth assignments,
…
For $n$ , there are $2^n$ possible truth assignments,

The complexity is exponential. To be understand here as “explosive”.

Question

If we consider a vocabulary composed with 8 propositional constants, what is the total number of possible truth assignments?

2.1.3.2. Definition of logical operators¶

A semantic is given to each operators: $\lnot$ , $\land$ , $\lor$ , $\Rightarrow$ , $\Leftrightarrow$ and $\oplus$

2.1.3.2.1. Negation¶

This is the only unitary operator (working with a unique proposition) noted $\lnot p$ . The truth table for negation (NOT) is:

$p$	$\lnot p$
0	1
1	0

It is interesting to remark that $\lnot\lnot p = p$

2.1.3.2.2. Conjunction $\land$ ¶

Conjunction of two propositions $p$ and $q$ is noted $p \land q$ . Evaluation of this propositional formula is true only if $p$ and $q$ are true. The corresponding truth table for conjunction (AND) is:

$p$	$q$	$p \land q$
0	0	0
0	1	0
1	0	0
1	1	1

2.1.3.2.3. Disjunction $\lor$ ¶

Disjunction of two propositions $p$ and $q$ is noted $p \lor q$ . Evaluation of this propositional formula is false only if $p$ and $q$ are false. The corresponding truth table for disjunction (OR) is:

$p$	$q$	$p \lor q$
0	0	0
0	1	1
1	0	1
1	1	1

2.1.3.2.4. Exclusive disjunction $\oplus$ ¶

The exclusive disjunction of two propositions $p$ and $q$ is noted $p \oplus q$ . Evaluation of this propositional formula is true if only one of $p$ and $q$ is true. The corresponding truth table for exclusive disjunction (XOR) is:

$p$	$q$	$p \oplus q$
0	0	0
0	1	1
1	0	1
1	1	0

2.1.3.2.5. Implication $\Rightarrow$ ¶

Implication between two propositions $p$ and $q$ is noted $p \Rightarrow q$ . Evaluation of this propositional formula is false only if $p$ is true and $q$ is false. The corresponding truth table for implication (IMPLY) is:

$p$	$q$	$p \Rightarrow q$
0	0	1
0	1	1
1	0	0
1	1	1

2.1.3.2.6. Biconditional $\Leftrightarrow$ ¶

Biconditional between two propositions $p$ and $q$ is noted $p \Leftrightarrow q$ . Evaluation of this propositional formula is false if only one of $p$ and $q$ is false. The corresponding truth table for Biconditional (XNOR) is:

$p$	$q$	$p \Leftrightarrow q$
0	0	1
0	1	0
1	0	0
1	1	1

2.1.3.3. Other notations for operators¶

Sometimes, other notations can be found for operators:

$\lnot p$ can also be written $\overline p$
$p \land q$ can also be written $p \cdot q$
$p \lor q$ can also be written $p + q$

2.1.3.4. Evaluation of a compound proposition¶

Evaluate a compound proposition consists in determining the truth value of the compound proposition given a truth assignment.

This is done in practice by replacing proposition constants by there values in formula. For example, the evaluation of compound proposition Eq.2.1 under the truth assignment $(p = 0, q=1, r=0)$ is :

$\begin{array}{cc} F = & ((p\land q) \lor (\lnot r)) \Rightarrow p \\ & ((0\land 1) \lor (\lnot 0)) \Rightarrow 0 \\ & (1 \lor 1) \Rightarrow 0 \\ & 1 \Rightarrow 0 \\ & 0 \end{array}$

The evaluation of Eq.2.1 under the truth assignment $(p = 0, q=1, r=0)$ is false.

2.1.3.5. Truth tables for compounds propositions¶

truth tables for compounds propositions allows to determine exhaustively the truth values of compounds propositions for each possible truth assignment. They are build by adding as many columns as necessary to evaluate sub-propositions. As example, let us consider the propositional formula of Eq.2.1. The corresponding truth table is:

Table 2.1: truth table for Eq.2.1¶
$p$	$q$	$r$	$p \land q$	$\lnot r$	$(p\land q)\lor\lnot r$	$F$
0	0	0	0	1	1	0
0	0	1	0	0	0	1
0	1	0	0	1	1	0
0	1	1	0	0	0	1
1	0	0	0	1	1	1
1	0	1	0	0	0	1
1	1	0	1	1	1	1
1	1	1	1	0	1	1

Question

What is the evaluation of propositional formula F under the truth assignment (p=0, q=1, r=1) ?

2.1.3.6. Satisfaction¶

A truth assignment is said to satisfy a proposition if and only if the proposition is evaluated as true under that truth assignment.

A truth assignment is said to falsify a proposition if and only if the proposition is evaluated as false under that truth assignment.

A proposition is said valid if and only if it satisfies every truth assignment.
A proposition is said unsatisfiable if and only if it satisfies any truth assignment.
A proposition is said contingent if and only if some truth assignments satisfies it and some other falsifies it.

Here are some examples:

As example, the proposition defined in Eq.2.1 is contingent since 6 truth assignments satisfies the proposition and 2 falsifies it.
the formula $p \lor \lnot p$ is valid
the formula $p \land \lnot p$ is unsatisfiable

2.1.3.7. Natural language and logic¶

Propositional logic can be used to formalize natural language by encoding sentences and thus helps to solve logical problems.

Consider the following sentence: If a student does not work hard in physics or in informatics, he will not become an engineer. This sentence is composed with 3 statements:

p: student works hard in physics
i: student works hard in informatics
e: student will become an engineer

This sentence can be easily traduced in propositional logic by the formula:

$\lnot p \lor \lnot i \Rightarrow \lnot e$

2.1.4. Propositional Analysis¶

2.1.4.1. Logical equivalence¶

The logical equivalence can be intuitively understand: Two propositions are equivalent if they says the same thing.

Two propositions F and G are thus said logically equivalent if and only if every truth assignment that satisfies F satisfies G and every truth assignment that satisfies G satisfies F. In that case we will write:

$F \equiv G$

It is possible to check the equivalence between two propositions by determining their truth tables and compare results.

Caution

Logical equivalence is a semantic equivalence that should not be confused with biconditional that is a syntax operator for logical propositions.

2.1.4.2. Logical properties¶

It is possible to demonstrate an important number of logical properties. Thus, we have:

2.1.4.2.1. Commutation¶

conjunction and disjunction operators can commute:

$\begin{array}{ccc} p \land q & \equiv & q \land p \\ p \lor q & \equiv & q \lor p \end{array}$

2.1.4.2.2. Association¶

conjunction and disjunction operators are associative:

$\begin{array}{ccc} (p \land q) \land r & \equiv & p \land ( q \land r) \\ (p \lor q) \lor r & \equiv & p \lor ( q \lor r) \end{array}$

2.1.4.2.3. Distribution¶

conjunction and disjunction operators are distributive:

$\begin{array}{ccc} p \land (q \lor r) & \equiv & (p \land q) \lor( p \land r) \\ p \lor (q \land r) & \equiv & (p \lor q) \land( p \lor r) \end{array}$

2.1.4.2.4. Neutral elements¶

true is neutral for conjunction and false is neutral for disjunction:

$\begin{array}{ccc} p \land true & \equiv & p \\ p \lor false & \equiv & p \end{array}$

2.1.4.2.5. Absorptive elements¶

false is absorptive for conjunction and true is absorptive for disjunction:

$\begin{array}{ccc} p \land false & \equiv & false \\ p \lor true & \equiv & true \end{array}$

2.1.4.2.6. Elimination of logical operators¶

Some operators can be eliminate to the profit of others. This is the case for implication, biconditional and exclusive disjunction:

$\begin{array}{ccc} p \Rightarrow q & \equiv & \lnot p \lor q \\ p \Leftrightarrow q & \equiv & (p \Rightarrow q) \land (q \Rightarrow p) \\ p \oplus q & \equiv & \lnot (p \Leftrightarrow q) \end{array}$

2.1.4.2.7. Morgan’s laws¶

$\begin{array}{ccc} \lnot (p \land q) & \equiv & \lnot p \lor \lnot q \\ \lnot (p \lor q) & \equiv & \lnot p \land \lnot q \end{array}$

2.1.4.3. Full system of operators¶

A system of logical operators is said functionally complete on a propositional language if every logical formula of this language can be expressed in terms of this system’s operators.

If we consider a finite domain of propositional constants, ie. $\mathcal{V}=\{ p_1,p_2, .. p_n \}$ and $\mathcal{F}$ representing the domain of propositional formulas that can be build on this vocabulary.

We can say that the system $S=\{ \lnot, \land, \lor\}$ is functionally complete. This can be demonstrate easily from properties of section Elimination of logical operators.
$\{ \lnot, \land\}$ and $\{ \lnot, \lor\}$ are also functionally complete systems.

2.1.4.3.1. The NAND and NOR operators¶

The NAND and NOR operators respectively for ‘not and’ and ‘not or’ are defined by the following truth table:

$p$	$q$	$p \text{ NAND } q$	$p \text{ NOR } q$
0	0	1	1
0	1	1	0
1	0	1	0
1	1	0	0

Systems {NAND} and {NOR} are functionally complete and are used for digital circuits.

2.1.4.4. Normal forms¶

A clause containing only the $\lor$ connector between propositional constants (or their negation) is called a disjunctive clause, also called maxterm.

A clause containing only the $\land$ connector between propositional constants (or their negation) is called a conjunctive clause, also called minterm.

Let us consider a propositional formulae F composed with propositional constants of vocabulary $\mathcal{V}=\{ p_1,p_2, .. p_n \}$ .

We call disjunctive normal form (DNF) of propositional formulae F, the propositional formula $F_D$ semantically equivalent to F and that is a disjunction of conjunctive clauses relative to F.

We call conjunctive normal form (CNF) of propositional formulae F, the propositional formula $F_C$ semantically equivalent to F that is a disjunction of conjunctive clauses relative to F.

A propositional formulae F admit a unique CNF and a unique DNF.

Writing the CNF or DNF of a propositional formulae is a way to determine if it is valid or unsatisfiable. It can be easily done using properties of section Logical properties

2.1. Propositional Logic¶

2.1.1. Intuitive approach¶

2.1.2. Propositional syntax¶

2.1.2.1. Proposition constant¶

2.1.2.2. Compounds propositions¶

2.1.2.3. Vocabulary and language¶

2.1.2.4. Tree representation¶

2.1.2.5. Operator precedence¶

2.1.3. Propositional semantics¶

2.1.3.1. Truth assignment¶

2.1.3.2. Definition of logical operators¶

2.1.3.2.1. Negation¶

2.1.3.2.2. Conjunction ¶

2.1.3.2.3. Disjunction ¶

2.1.3.2.4. Exclusive disjunction ¶

2.1.3.2.5. Implication ¶

2.1.3.2.6. Biconditional ¶

2.1.3.3. Other notations for operators¶

2.1.3.4. Evaluation of a compound proposition¶

2.1.3.5. Truth tables for compounds propositions¶

2.1.3.6. Satisfaction¶

2.1.3.7. Natural language and logic¶

2.1.4. Propositional Analysis¶

2.1.4.1. Logical equivalence¶

2.1.4.2. Logical properties¶

2.1.4.2.1. Commutation¶

2.1.4.2.2. Association¶

2.1.4.2.3. Distribution¶

2.1.4.2.4. Neutral elements¶

2.1.4.2.5. Absorptive elements¶

2.1.4.2.6. Elimination of logical operators¶

2.1.4.2.7. Morgan’s laws¶

2.1.4.3. Full system of operators¶

2.1.4.3.1. The NAND and NOR operators¶

2.1.4.4. Normal forms¶

2.1.3.2.2. Conjunction $\land$ ¶

2.1.3.2.3. Disjunction $\lor$ ¶

2.1.3.2.4. Exclusive disjunction $\oplus$ ¶

2.1.3.2.5. Implication $\Rightarrow$ ¶

2.1.3.2.6. Biconditional $\Leftrightarrow$ ¶