2.2. Binary encoding¶

Informatics systems are treating a lot of information (sensors, text, images, musics, videos, games, etc.) called data. Whatever the form of the data is, everything on a computer is encoded as numbers, such that a computer is finally a big calculator with specific input and output peripherals (keyboard, screen, etc.).

2.2.1. Encoding using numbers¶

Whatever the origin of the data is, the computer is treating it as numbers. Here are presented some examples of existing encoding.

2.2.1.1. Encoding text¶

The simpler way to encode a text is to associate an integer number to each possible character. For example, in the English language, there are 26 letters and some special characters (%<,;:! etc.). The ASCII code is encoding characters with a value range between 0 and 127.

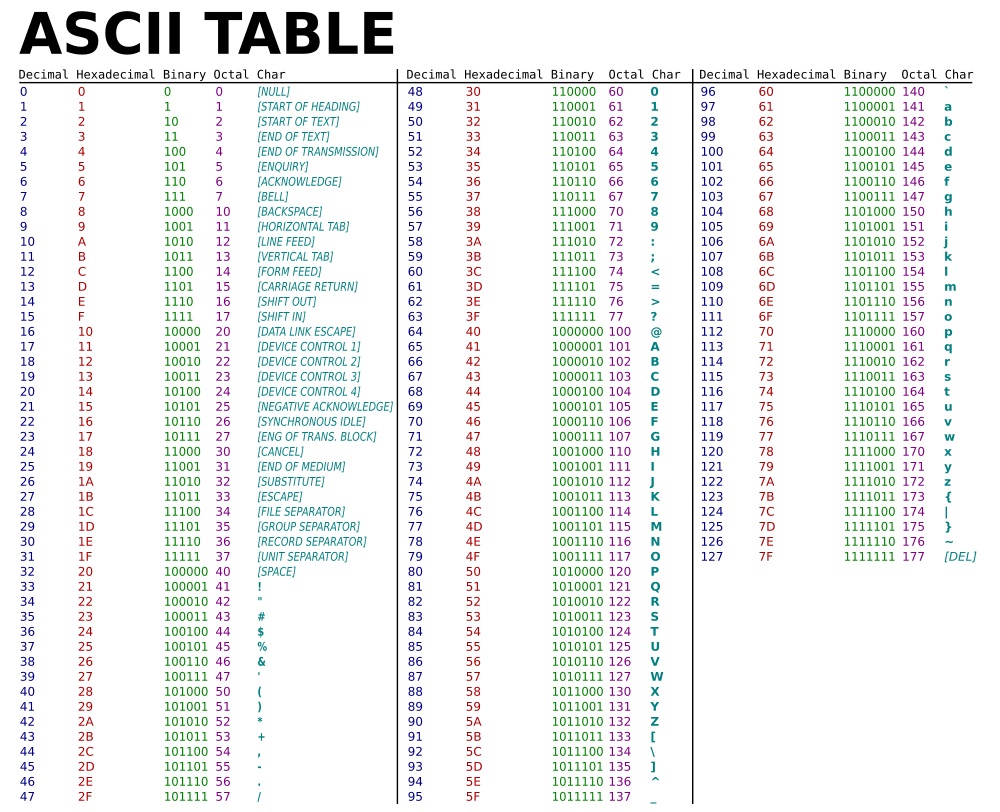
Figure 2.2: ASCII table for character encoding¶

As example, we see that the ‘a’ character is represented by the number 97 in the ASCII table.

2.2.1.2. Encoding images¶

For images, this is similar to text. An image is discretized in pixels. Typically, a full HD image is composed with 1920 x 1080 pixels, that is to say more than 2 million pixels. A pixel is a small square with a unique value for each primary colors (Red, Green and Blue) ranged between 0 and 255.

Figure 2.3: RGB encoding example (https://htmlcolorcodes.com/fr/)¶

2.2.1.3. Other encoding examples¶

Other information are also encoded:

A sound needs pitch and intensity encoding.
A video is composed with a lot of images.

2.2.2. Binary algebra¶

Thus, each data of informatics systems are encoded as numbers. But how these numbers are stored themselves physically in an electronic system ? This is ensured thanks to electronic components that may let a current pass (1) or not (0) acting like switches. For example, a unique switch is able to encode 2 different information:

the switch is open: the current do not pass (0)
the switch is closed: the current pass (1)

If we use a second switch, 4 different information may be encoded:

switch A is open:
- switch B is open: (00)
- switch B is closed: (01)
switch A is closed:
- switch B is open: (10)
- switch B is closed: (11)

With n switches, $2^n$ different information may be encoded.

In informatics the elementary data that can be stored electronically is named a bit and can be set to 0 or 1.

8 bits are grouped to form a byte.

Question

How many bytes are necessary to encode 256 different information (i.e. for example to store one primary color in the RGB encoding) ?

2.2.2.1. Encoding positive integers¶

Binary encoding of positive integers is the more natural. Let us consider that the information to store is encoded on 8 bits (or 1 byte), the range of integer will be from 0 to $2^8 - 1 = 255$ .

integer	binary encoding
0	00000000
1	00000001
2	00000010
3	00000011
4	00000100
5	00000101
…	…
255	11111111

To generalize, every integer may be written as a sum of power of 2.

$\forall i \in \mathbb{N}, i = b_0 2^0 + b_1 2^1 + b_2 2^2 + ... + b_n 2^n$

The binary representation of an integer is thus:

bn

…

b2

b1

b0

Integers are generally encoded on 4 bytes (32 bits).

2.2.2.1.1. Convert an integer in binary¶

To convert easily an integer in binary, a simple way is to apply successive entire division by 2. As example, let us consider the number 156:

operation	quotient	remainder
156/2	78	0
78/2	39	0
39/2	19	1
19/2	9	1
9/2	4	1
4/2	2	0
2/2	1	0
1/2	0	1

$156 = 0 \times 2^0 + 0 \times 2^1 + 1 \times 2^2 + 1 \times 2^3 + 1 \times 2^4 + 0 \times 2^5 + 0 \times 2^6 + 1 \times 2^7$

1

0

0

1

1

1

0

0

exercise

How many bytes are necessary to store complete information of an image in full HD (1920 x 1080 colored pixels) ?

2.2.2.2. Encoding negative integers¶

Several methods exist to encode a negative number, but the more efficient is those using the two’s complement and act in three steps:

The absolute value of the number is encoded in binary.
All bits are reversed (0 becomes 1 and reversely).
1 is added to the result.

As example, the negative number -42 will be encoding by these three steps:

	b6	b5	b4	b3	b2	b1	b0
step 1	0	1	0	1	0	1	0
step 2	1	0	1	0	1	0	1
step 3	1	0	1	0	1	1	0

2.2.2.3. Encoding real numbers¶

Real number are encoded thanks to the IEEE754 standard using 32 bits (4 bytes). The objective is to express the real number using a scientific representation in binary. The steps are:

The real number is decomposed in power of 2 the entire and decimal part of the real number.
The binary encoding is then normalized in scientific form.
The first bit is used for the sign (0 for positive real number). The mantissa is using 23 bits and the exponent is augmented by 127 and encoded on 8 bits.

Let us take an example: the number 197,75.

$\begin{array}{ccc} 197,75 & = & 128 + 64 + 4 + 1 , 0.5 + 0.25 \\ & = & 2^7 + 2^6 + 2^2 + 2^0, 2^{-1} + 2^{-2} \\ & = & 11000101,11 \\ & = & 1,100010111 \times 2^7 \end{array}$

The binary representation of 197,75 is then:

sign (b31)	exponent (b23 to b30)	mantissa (b0 to b22)
0	10000110	10001011100000000000000